対数、指数っぽい関数を考える
- created
- 2017-04-22
- last change
- 2017-06-07 21:49:51 +0000
思いついた
\(0 \to 1\)の間で指数/対数っぽいカーブをする関数一般的に利用しやすいやつなにかないかと考えていた時、
べき乗使えばいいんでね!? ってなった。
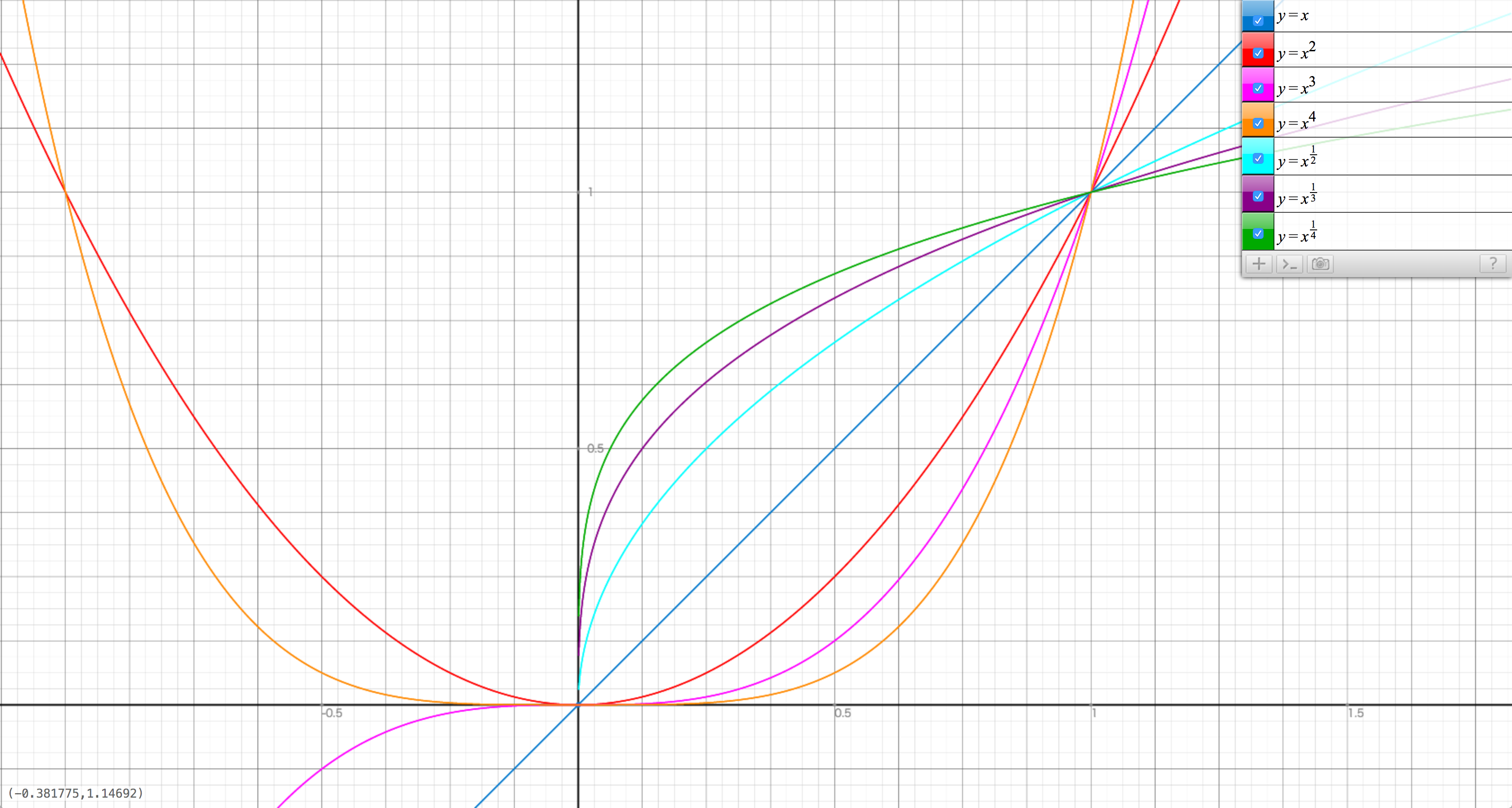
なぜかというと \(y = x^n \) の時
- \( x = 0 \) の時必ず \( y = 0 \)
- \( x = 1 \) の時必ず \( y = 1 \)
- \( n = 1 \) の時、\( y \) は \( x \) に比例
- \( n \gt 1 \) の時は指数っぽい曲線になる
- \( 0 \lt n \leqq 1 \) の時は対数っぽい曲線になる
- 対数曲線 \( log_{a}x \)、指数曲線 \( a^x \) と関数を分けることなく使える
ちなみに \( 0 \lt n \leqq 1 \) のべき乗というのは平方根などになる。 \[ x^\frac{1}{n} = \sqrt[n]{x} \]
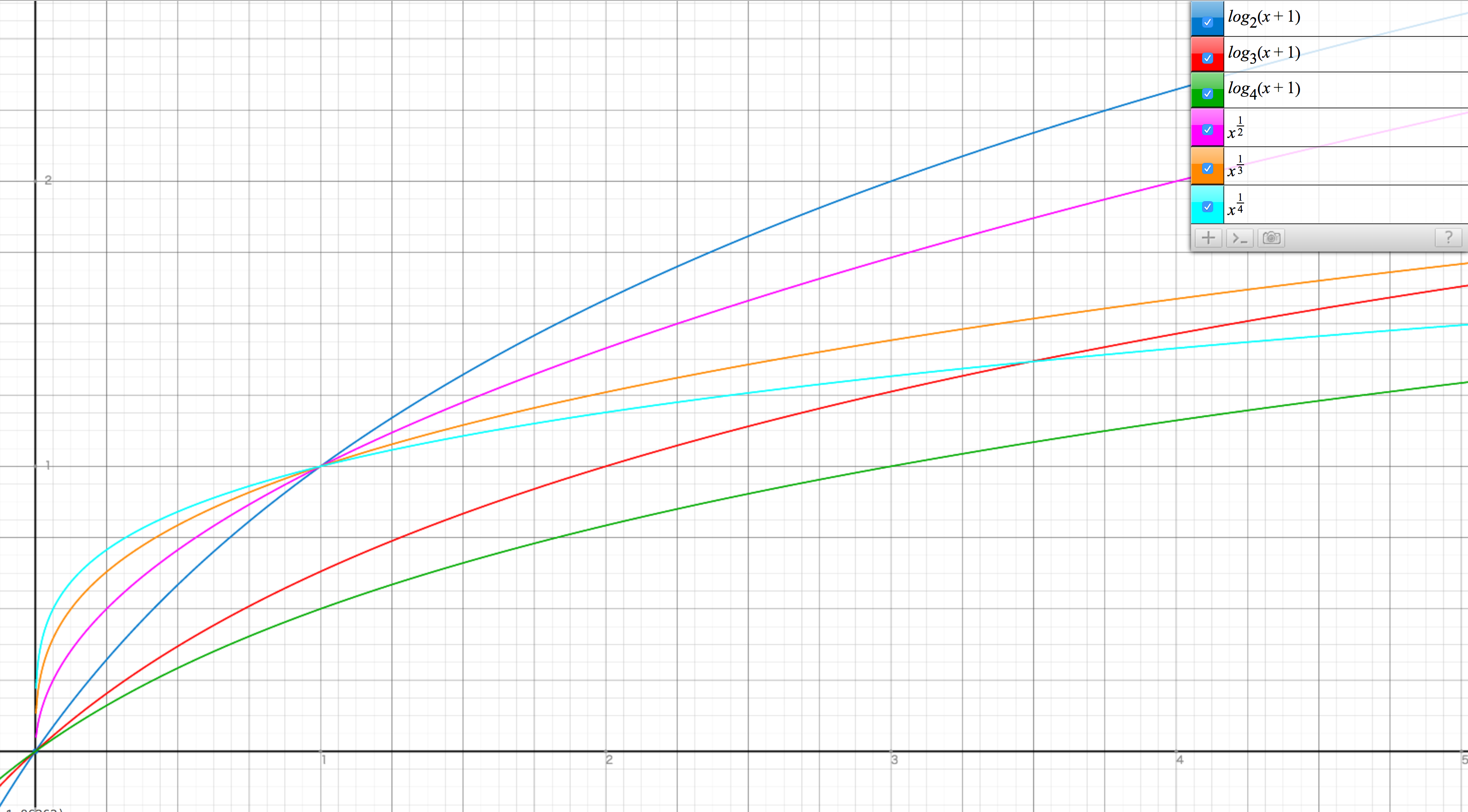
\( log_{a}x \)との比較
安直に \( x^{\frac{1}{n}} \) とすると\( log_{a}x \) に比べ急峻なカーブになる。 この辺りは感覚で調整してゆくしかないか。